【磁共振实验室：卢星宇博士 撰文】【仪器设备：600 MHz / 500 MHz 核磁共振波谱仪】【地点：4号楼102室 磁共振实验室】

扩散核磁共振实验根据样品体系不同的自扩散系数（取决于分子的大小和形状）在核磁谱上直接分辨混合物中的不同化合物。扩散核磁共振可用于解析混合物的复杂谱图，也可用于确定分子和聚集体的大小，确定聚合度、溶剂化壳的尺寸或其他微观结构。生成的核磁谱图在某些方面类似于色谱图，同时也提供了高分辨的核磁共振信息，可用于单个组分的结构归属（Figure 1）。然而，对于大多数混合物，其分辨率不足以进行直接归属，需要应用核磁共振色谱技术。

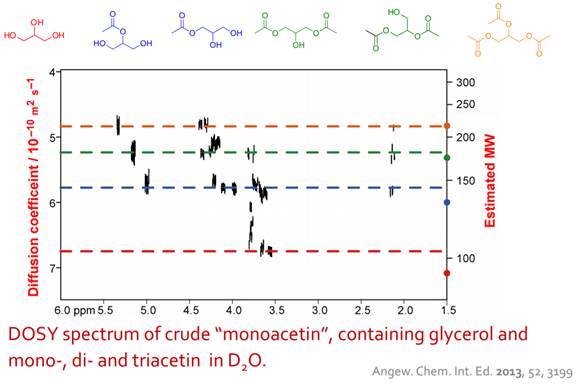
Figure 1. A representative application of diffusion NMR for structural analysis of mixture.

扩散核磁共振技术通常被称为自扩散（SD）-核磁共振或更常见的扩散排序谱（DOSY）。这是通过将常规核磁共振波谱中使用的射频脉冲与空间信息编码的磁场梯度相结合来实现的。在脉冲梯度扩散实验的最简单形式（以后将介绍更复杂的实验）中，称为脉冲场梯度回波（PGSE，Figure 2），用90°射频脉冲激发磁化矢量，然后用磁场梯度脉冲分散。经过一段Δ/2的时间，一个180°的射频脉冲将分散的磁化矢量反转，使得经过一段时间Δ后，磁化强度为梯度脉冲后的负值。此时，应用第二梯度脉冲来重新回聚信号。

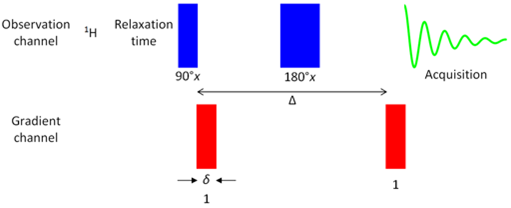
Figure 2. Pulse sequence for gradient PGSE.

信号回聚只对那些没有明显上下移动的原子核实现。扩散导致一些原子核（分子）离开其信号可以重新回聚的地方，从而导致降低信号强度（Figure 3）。磁场梯度脉冲越强、时间越长，其空间选择性越强、产生的信号越弱。磁场梯度脉冲的强度和持续时间决定了原子核能够扩散并仍然产生信号的距离。磁场梯度强度对信号强度的影响，就聚焦在没有扩散超出范围的分子上：梯度越大，范围越小；梯度越小，范围越大。

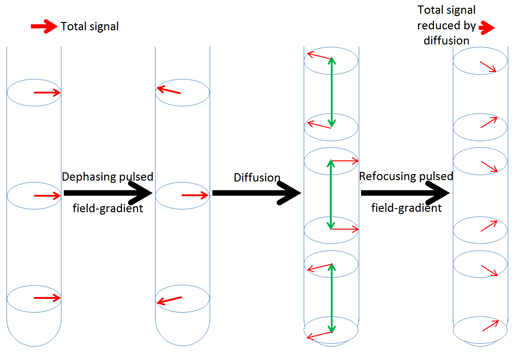
Figure 3. Effect of diffusion combined with magnetic field gradient pulses. The physical movement of nuclei reduces the effectiveness of the refocusing pulse reducing the resulting signal strength.

脉冲序列被重复多次（通常16-64次）采样以增加梯度强度（Figure 4）、并保持延迟不变。信号强度与梯度强度的关系图如Figure 4（右）。强度I与γ为旋磁比（对质子来说为4257 s-1 G-1）的情况成正比，G为梯度强度，δ和Δ为脉冲延迟，D为自扩散常数。扩散常数可以通过拟合高斯衰减的非线性曲线来获取。在这种情况下，曲线是与成比例的。因此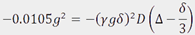，扩散常数可以计算如下：

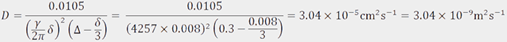
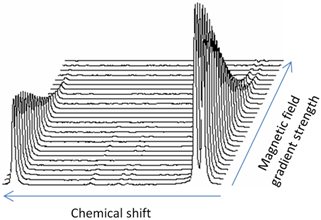
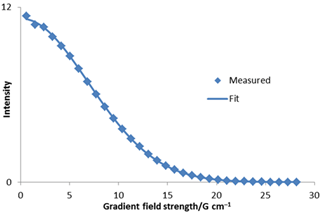
Figure 4. In this diffusion spectrum, the peak on the left decays faster with increasing gradient strength and has a higher diffusion constant than the peaks on the right. Gaussian fit to diffusion peak intensity using a non-linear fit.

扩散速率也可以通过线性拟合ln（I）和g2来计算（Figure 5）。在这种情况下，得到3.13×10–9 m2 s–1的值。这与非线性拟合非常相似，计算起来更容易，但精度较低，因为各点的分布不均匀，ln（I）的精度也不相同。信号通常重叠或来自多个环境。在这种情况下，会产生大高斯或多高斯衰变。这可以使用非线性拟合进行分析，而不适合线性分析。在Figure 5（右）中，红色和绿色高斯曲线相加以拟合实验数据。为了得到扩散常数，可以利用拉普拉斯变换（ILT）的非线性反演来提取高斯衰减常数。衰变常数除以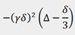，通常绘制在对数刻度上以使它们更清晰，因为扩散速率通常变化几个数量级。

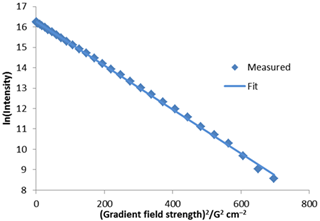
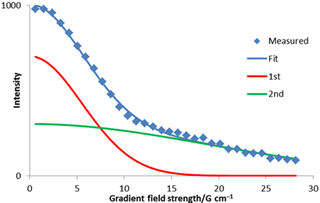
Figure 5. Linear fit to diffusion peak intensity (left) and Bigaussian fit to diffusion peak intensity using a non-linear fit (right).

扩散谱通常表示为横坐标为化学位移和纵坐标为对数（扩散常数）的二维图（Figure 6），称为扩散排序谱（DOSY）。通过在频域产生高分辨率的傅里叶变换，可以很容易地分析采样维。然而，扩散维的分析涉及拉普拉斯变换（ILT）的反演。虽然对于单个衰变来说，这是相当精确的，高达2%，但当分离两个或更多重叠信号时，它的分辨率非常低，几乎不可能分辨出重叠频率相差小于30–50%的信号扩散。DOSY谱的每个导出片段对应于一个组分的常规核磁共振谱（Figure 7）。各成分的扩散速率可从DOSY谱中读取（Figure 6和Table 1）。

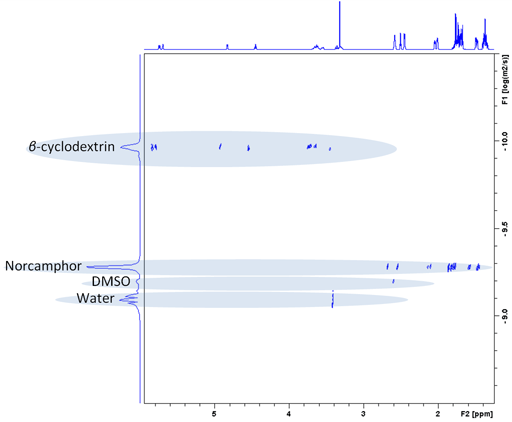
Figure 6. DOSY spectrum of norcamphor and β-cyclodextrin in DMSO-d6.

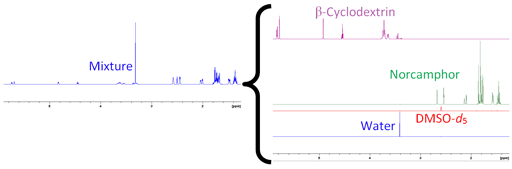
Figure 7. Individual spectra extracted from a DOSY spectrum of norcamphor and β-cyclodextrin in DMSO-d6.

Table 1. Diffusion rates measured from the DOSY spectrum of norcamphor and β-cyclodextrin in DMSO-d6.